探索アルゴリズムを視覚的に比較

非常に面白い。ためになるので掲載

http://gigazine.net/news/20150619-search-algorithm-visualize/




出発点(問題)とゴール(解)が用意された時にどのような道順で進めばいいか調べるアルゴリズムが「探索アルゴリズム」です。この探索アルゴリズムには複数の種類が存在するのですが、中でも基本的なもの8つ＋ゲームデベロッパーの＠shohei909さん自作のアルゴリズム2つを合わせた全10種のアルゴリズムで迷路をクリアしようとすると、どのような探索が行われることになるのかを目で見て楽しめるようにしたのが「迷路で眺める探索アルゴリズム」です。

迷路で眺める探索アルゴリズム(Search algorithm visualize) - wonderfl build flash online
http://wonderfl.net/c/hq8p

迷路で眺める探索アルゴリズム | 机上のにゅーろん
http://spheresofa.net/blog/?p=1044

これが「迷路で眺める探索アルゴリズム」。


画面上部にはこんな感じの操作メニューが敷き詰められており……


赤枠部分から探索アルゴリズムを変更可能。使用可能なアルゴリズムは深さ優先・幅優先・反復深化深さ優先・山登り優先・最良優先・間違い制限・幅優先ビーム・最良優先ビーム・優良優先・二重制限の10種類あり、画面上部からいつでも選択できます。


「new」をクリックすればいつでも迷路の形を変更可能で、「speed」を調整してアルゴリズムが迷路を探索するスピードを調整することもできます。


「start」をクリックで探索がスタート。「＜＜」で探索のスタート時点に戻る、「＜」でひとつ前の段階に戻る、「＞」でひとつあとの段階に進む、「＞＞」で探索の終了時点に移動。


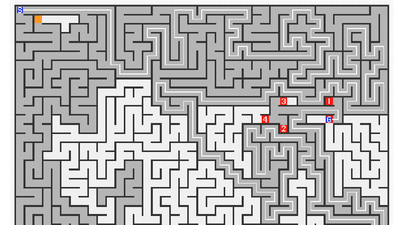
「S」と書かれた青色のマスがスタート地点


「G」と書かれた青色のマスがゴール地点


迷路自体はこんな感じ。薄いグレーが未探索部分で、濃いグレーが探索済の部分。


赤色マスは探索で発見した分岐点あるいは行き止まり


オレンジのマスは「不要な探索」と見なされ打ち切られた「枝刈り」の分岐点・行き止まりで、赤色マスに書かれた数字はゴールに近い順番に順位を付けたもの。


探索が終了すると迷路上に白色の線でゴールまでの道のりが記されます。濃いグレー色の部分は探索済みの箇所になるので、ゴールにたどり着くためにかなり無駄な探索を行ったことが分かります。


そして、迷路下部には「分岐数」や「探索回数」が書かれており、探索回数は迷路内で移動した回数、つまりは計算時間(CPU Time)に直結。そして、分岐数は探索中に発見した赤マスの数で、メモリの使用量に直結します。


実際に「深さ優先探索」で迷路をクリアするまでの探索の様子は以下のムービーで見られます。

「迷路で眺める探索アルゴリズム」を使ってみた - YouTube


というわけで、同一の迷路を各アルゴリズムがクリアすると、クリアまでの時間や分岐数、探索範囲などがどれくらい異なってくるのか調べてみました。

◆深さ優先探索(Depth-first search)


分岐数：8、探索回数：803、最大分岐数：15

10個のアルゴリズムの中で最大分岐数が最大。

◆幅優先探索(Breadth-first search)


分岐数：7、探索回数：820、最大分岐数：9

迷路をクリアしたアルゴリズムの中で最も多くの探索回数を要した。

◆反復深化深さ優先探索(Iterative deeping depth-first search)


分岐数：8、探索回数：775、最大分岐数：12、深さ制限：316

◆山登り法(Hill climbing)


分岐数：0、探索回数：19、最大分岐数：2

唯一迷路をクリアできない探索アルゴリズム

◆最良優先探索(Best-first search)


分岐数：10、探索回数：411、最大分岐数：10

10種類の中でも特に探索回数が少なくて済むアルゴリズム。

◆間違い制限探索(Limited discrepancy search)


分岐数：11、探索回数：600、最大分岐数：12、間違い制限：10

こちらも比較的探索回数が少なめ。ただし、分岐数は迷路をクリアしたアルゴリズムの中で最大。

◆幅優先ビームサーチ(Breadth-first beam search)


分岐数：5、探索回数：682、最大分岐数：7

分岐数のみ最小。

◆最良優先ビームサーチ(Best-first beam search)


分岐数：5、探索回数：394、最大分岐数：6

迷路をクリアした中では探索回数・分岐数共に最小。

◆優良優先探索(good-first search)


分岐数：7、探索回数：814、最大分岐数：8

◆二重制限探索(Double limit search, Good-first beam search)


分岐数：7、探索回数：809、最大分岐数：8

探索アルゴリズムによって迷路を探索するルートはかなり異なってくるようで、迷路の形次第では探索済ゾーンの形は大きく変わってきます。なお、「迷路で眺める探索アルゴリズム」で使用されている探索アルゴリズムは迷路だけでなくパズルやソリティアなどのゲームの探索に利用可能で、手を加えればチェスやオセロのような対戦ゲームに応用することもできるそうです。